Understanding Current Dividers: The Basics Explained for Beginners

Current Dividers Explained!

Introduction

A current divider is a type of circuit where a single current input is divided among multiple branches or paths. The value of each current path depends on the resistance of each branch, which is determined by the current divider rule.

Understanding the Current Divider Rule

The current divider formula is essential in calculating the current that flows through the individual resistors in a parallel circuit.

A couple of things to note when working with the current divider law. Such include:

• It has to be a parallel circuit. This is where multiple components, such as resistors, are connected in parallel to each other, leading to multiple paths for current flow.
• The input current from the source is split to flow in different paths depending on the number of paths available in the circuit.
• You also need the resistance in the paths to find out how much current is using a particular path. The amount of current flowing in a path is inversely proportional to the resistance of the branch. For example, lower resistance means more current will flow and vice versa.
• In the current divider equation, the voltage in the parallel circuit is the same across each branch.
  

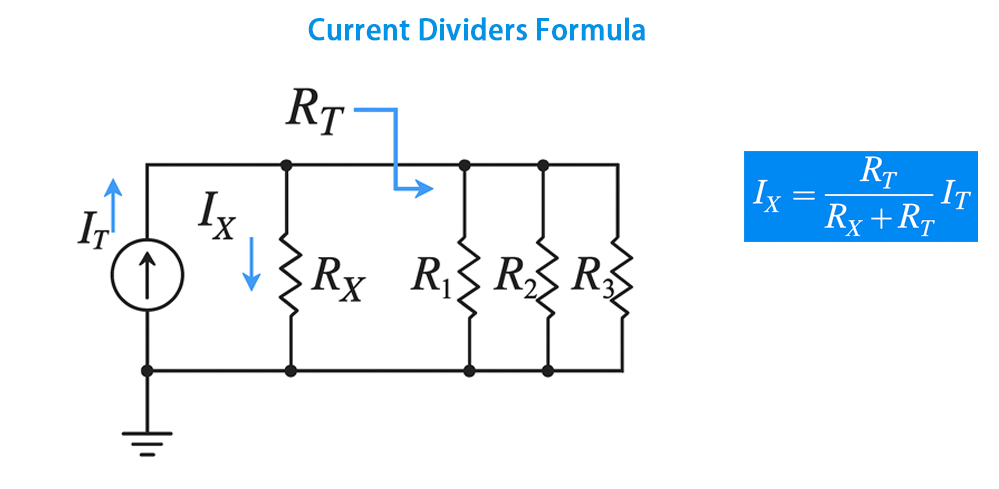
The current divider formula is easy to follow and use when you have all the relevant values of the different parts of the circuit.

The formula is: I_branch = I_source * (R_total / R_branch )

I_branch – this represents the current flowing through a particular path

I_source – this is the value of the current flowing from the source

R_total – this is the total resistance in the parallel circuit

R_branch – this is the resistance of the branch you want to determine I_branch

It becomes easy to replace the values depending on the path you want to evaluate to find the current in that branch.

Practical Use Cases of a Current Divider

Understanding the current divider rule equation can lead to working with it in many applications. Some of the applications include:

• Power distribution systems require a balanced distribution of current across the different parallel lines. This prevents voltage drops and overheating.
• Automotive systems could also use current dividersto manage the current flow of various components. For example, the dashboard, sensors, and headlights all need different amounts of current, thus needing a current divider.
• Electrical meters also need current dividers to control the current flow and ensure precise measurements. This allows the meters to handle large currents while maintaining safe operation easily.
• Audio systems need such a circuit to control the speaker volume and other connected devices through current flow regulation.
• We cannot forget the light circuits, in which each bulb receives the correct amount of current based on the current divider. The same can be used to control brightness and prevent potential overloads.
• A current divider circuitcan also be used for general-purpose applications where the current flow through some components needs to be reduced.

Pros and Cons of the Current Divider Rule

Pros

The formula for current divider is simple to understand, and you can easily handle current distribution in parallel circuits. This makes it easier to work with than similar equations, such as Kirchhoff’s Current Law.

The formula helps you find uneven loading and correct it to ensure proper loading and reduce the chances of overcurrent. Even when the circuit has different resistance paths, it is possible to accurately predict the current flowing through them and take measures to avoid uneven loading.

You can also manage power dissipation better in circuits with this equation. There are cases where engineers manage power dissipation better in high-power applications such as motor control systems with this formula.

Cons

The biggest downside is that the current divider rule calculator is limited to parallel circuits. When the circuit gets complex, the equation is less effective.

You also have to work with ideal conditions and assumptions. For example, you assume there is uniform voltage and negligible impedance variations, which sometimes cannot hold in some cases.

Mistakes to Avoid When Working with Current Dividers

Sometimes, your mistakes can lead to incorrect calculations using a current divider calculator. The first mistake is only using resistance when working with AC circuits. This is because you need to consider impedance rather than resistance for an AC circuit. Impedance is the combination of reactance and resistance. So, replace resistance with impedance in the current divider rule for AC circuits.

The second mistake is incorrectly identifying the parallel branches of the circuit. Keep in mind that the current divider rule only applies to the parallel branches. If you cannot accurately determine the paths, the values you get for the current flowing in a branch will be incorrect.

The other mistakes include:

• Using very high or low resistor values
• Ignoring resistor tolerances as they affect the accuracy of the current distribution calculation
• Ignoring environmental factors such as temperature and aging, which can affect the performance of the components

Current Divider vs. Voltage Divider: Understand The Difference

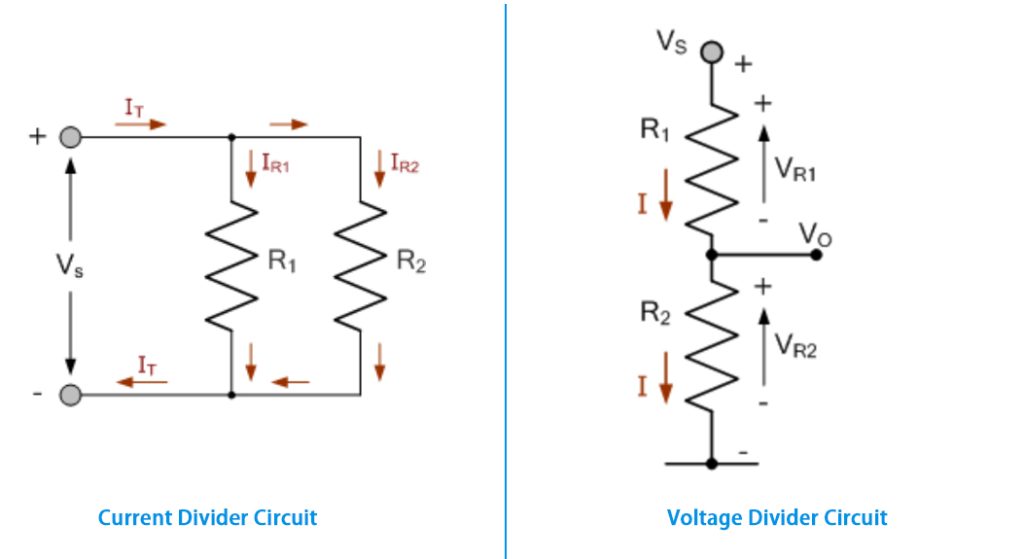
Now that you know what is a current divider, it is possible you may have come across a voltage divider formula, and you are now wondering what the difference is.

The biggest difference is in the circuit configuration.

The resistors are connected in parallel for the current divider and in series for the voltage divider.

Another difference is how the current and voltage behave in the circuit.

In a current divider, the current from the source is divided among the circuit’s branches depending on each branch’s resistance level.

The voltage divider circuit does the same, but the voltage is divided proportionately to the resistance value.

Application

Current dividers are primarily used for applications that limit current through a specific branch. As for the voltage dividers, they are used mostly for adjusting or scaling down voltage across different components.

How to Simulate a Current Divider Circuit

Simulating a current divider circuit can help you understand it better. There are a couple of ways of doing this. One is to use software such as Multisim or CircuitLab to generate and simulate the circuit, or you can build a physical circuit containing resistors and a voltage source.

If you decide to choose software simulation, make sure you install the right software and build the circuit in it. This included adding necessary components such as the voltage source, resistors, and sometimes an ammeter for measuring the current.

Connect the components in parallel in the software and set the correct values for the components. Once everything is connected, simply run the simulation and see how the software calculates the different current values.

Conclusion

Current and voltage dividers are crucial in designing circuits powering different devices. We have seen how a current divider would be ideal for restricting current flow in specific applications, which helps reduce cases of overcurrent. Depending on how the circuit is configured, expect to encounter many applications. Always take note of other parameters that can affect the accuracy of the current divider circuit.