PID Controllers Explained: The Ultimate Guide for Beginners

導入

あ PID controller is a control loop feedback mechanism commonly used in industrial control systems to regulate different types of process variables such as temperature, flow rate, speed, and pressure. The PID control system achieves its performance by comparing the actual value with the desired setpoint, calculating the error, and adjusting the output to minimize the error presented.

How Each Term Works

The terms PID in the PID control loop stand for proportional, Integral, and derivative.

Proportional (P) is the component that reacts with the current error directly. If there is a large error, this results in a larger output correction and vice versa.

The integral (I) is the component that accumulates the error over time. Its job in PID controllers is to eliminate steady-state errors and ensure the process variable reaches the setpoint eventually.

The Derivative (D) in the PID controller meaning is the component that anticipates any future errors based on how often the current error appears. Once it determines this rate of change in errors, it can help dampen oscillations and improve the response speed of the PID controller.

Once you combine these three actions, you will see how the PID controller is able to provide a robust and adaptable control solution for many industrial processes.

The PID Controller Equation

その formula for a PID controller helps understand how the three components work together to achieve the desired results. Here is the equation of a PID controller:

u(t) = Kp * e(t) + Ki * ∫e(t) dt + Kd * de(t)/dt

Each component has a role to play, and this is what to expect:

u(t) is the control output signal.

e(t) is the error signal.

Kp is the proportional (P) gain.

Ki is the integral (I) gain.

Kd is the derivative (D) gain.

∫e(t) dt is the integral of the error over time.

de(t)/dt is the derivative of the error with time.

Types of PID Controllers

理解できたと思います what is a PID controller, we can look at the various types available to see how you can apply them to different applications. Let us check them out below.

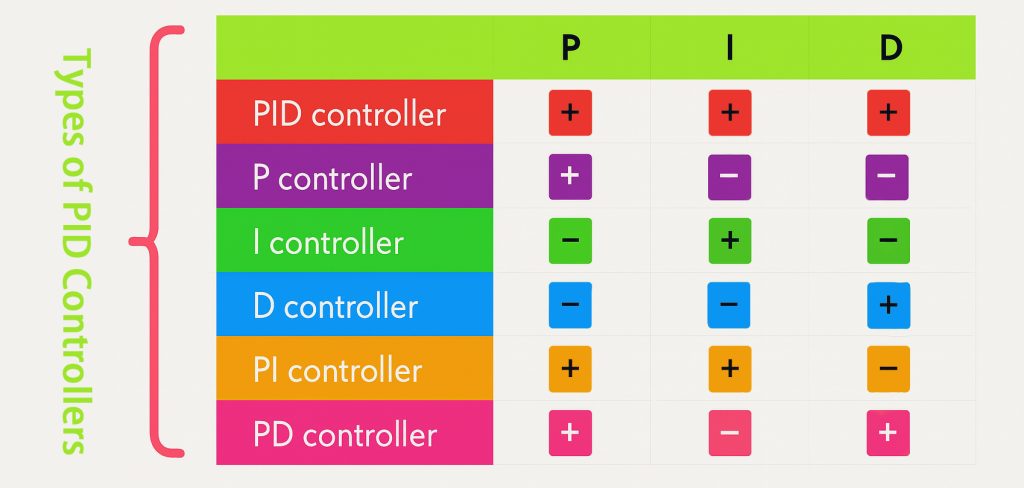
Proportional (P) Controller

This type of PID controller is a fundamental type of feedback controller that adjusts the output signal in proportion to the error signal. The error signal is the difference between the desired setpoint and the actual process variable.

The proportional gain will determine the overall sensitivity of the controller. Having a higher gain means a faster response, but it can also increase the overshoot and steady-state error. A lower gain, on the other hand, leads to a slower response but can reduce the steady-state error and overshoot.

This type of P controller requires manual tuning to help adjust the gain for optimal performance. This might prove challenging for some systems.

利点

• Simple to implement and understand
• Provides a fast response to the changes in a process
• Improves the stability of a system

Disadvantages

• Cannot eliminate the steady-state error
• May potentially lead to instability or oscillations in some systems
• Requires manual tuning

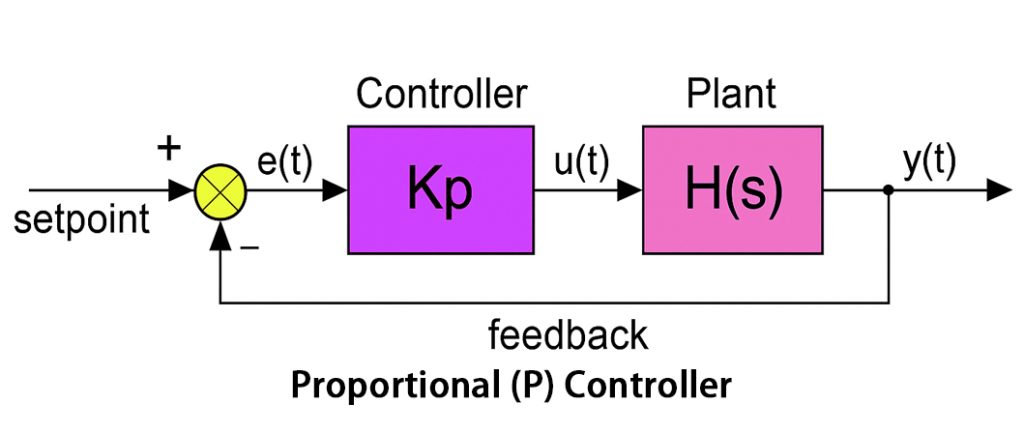
Integral (I) Controller

In this case, the control system adjusts its output depending on the integral of the error signal over time. Its job is to eliminate the steady-state errors in a control system. These are the errors you encounter when measuring the difference between the desired value and the estimated value.

このタイプの PID controller integrates the error to ensure that even small changes in the error will help drive it back towards the desired set point. It is expected that this controller will be slow to respond to sudden changes in the system.

When the integral gain is too high, the controller can lead to overshoot and oscillations. These could destabilise the system.

The I-controller is commonly used in applications such as temperature control, speed control, level control, and more.

利点

• Helps with eliminating the steady-state error
• Offers improved accuracy
• It can handle varying loads

Disadvantages

• May lead to overshoots and instability
• Tends to have sluggish responses
• It cannot be used alone in practical applications

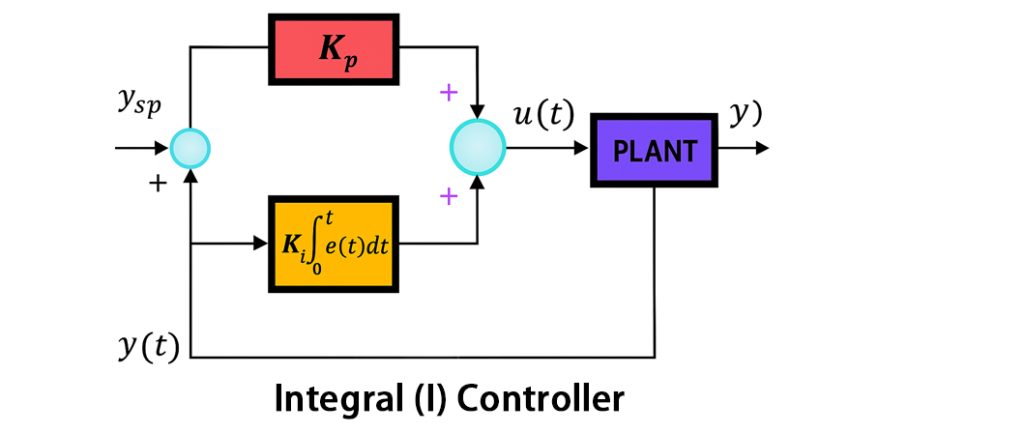
Derivative (D) Controller

The D controller works by responding to the rate of change of the error signal. Its job is to anticipate future errors by analyzing how quickly the error is increasing or decreasing, and then adjusting the control output to address the error. This action is crucial in damping oscillations and reducing instances of overshoot. It also helps improve the overall stability of the system.

Examples of applications include temperature control, quadcopters, and other systems that need precise and stable control.

利点

• Helps to reduce the overshoot
• Dampens the oscillations
• Improves the overall response time

Disadvantages

• It is sensitive to noise
• It cannot be used alone
• Can lead to issues in case of sudden setpoint changes

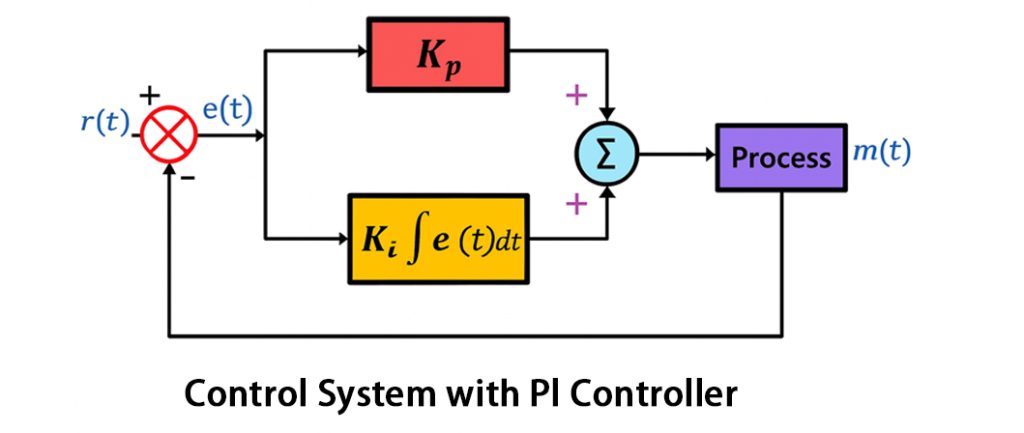
PI Controller

The PI controller combines both the proportional and integral control actions vital for regulating the system’s output and minimizing the error between the measured value and desired setpoint.

This controller operates by adjusting the system’s output based on the current error (proportional term) and accumulating past errors (integral term). When you have this combination, the response times are faster, and you can eliminate the steady-state error. This makes the PI controller widely used for controlling different types of industrial applications.

利点

• Eliminates the steady-state error
• Comes with a faster response time
• Offers simpler tuning options

Disadvantages

• Often has a high starting overshoot
• Can be sensitive to noise
• Limitations with nonlinearities

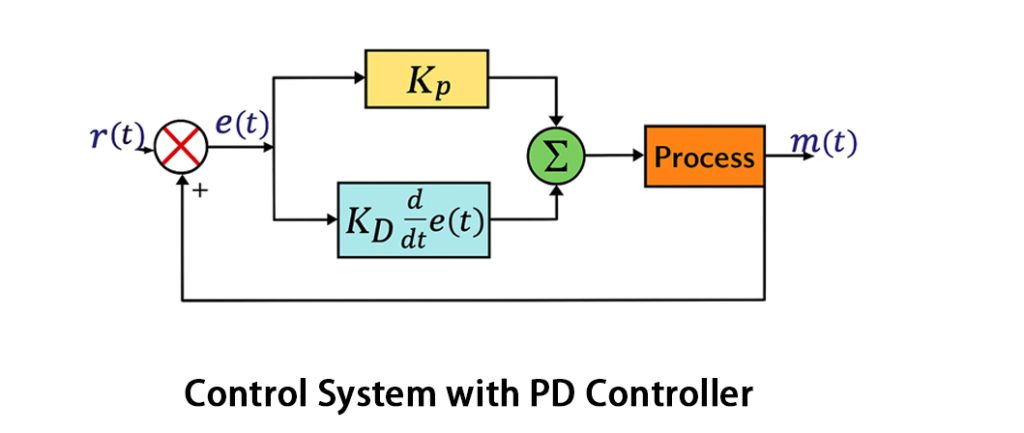
PD Controller

This is another type of PID controller that works by combining the proportional and derivative controls to adjust the system’s output. The work of the proportional control is to offer an immediate response to the error, while the derivative control anticipates future errors to help improve system stability and reduce overshoot.

When these two are combined, you can expect to have improved transient response as the PD controllers reduce the rise time, overshoot, and settling time. The result is a more stable and responsive system.

There are also reduced oscillations thanks to the derivative action. This helps dampen oscillations and stabilize the system. It helps prevent it from constantly overshooting and undershooting the setpoint.

Tuning is also necessary for the PD controllers. This helps the setup achieve the desired performance. Sometimes, having too much proportional gain leads to instability, while also too little derivative gain leads to insufficient damping.

利点

• There is improved stability
• You get a faster response time
• Expected reduced overshoot
• Simpler implementation

Disadvantages

• Inability to eliminate steady-state errors
• Can potentially amplify noise
• Not the best for all processes

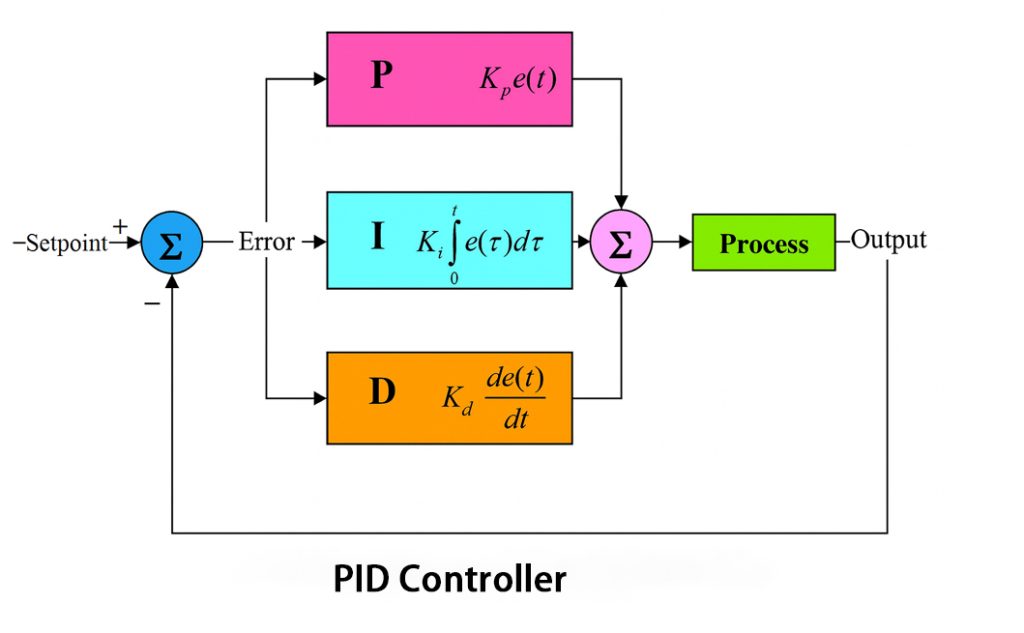
PID Controllers

In this case, all three terms are combined to form one system. You will have the proportional (P) term for responding to current errors by providing an immediate correction proportional to the magnitude of the error. The integral (I) term accumulates the past errors over time to help eliminate steady-state errors and ensure the process variable can eventually reach the desired setpoint.

The derivative (D) term responds to the rate of change of the error by anticipating future errors and dampening oscillations.

The common applications for PID controllers include temperature control, flow control, pressure control, speed control, and level control.

Tuning PID controllers is necessary to achieve the desired performance. This includes better stability, responsiveness, and minimal overshoot.

利点

• Simple and easy to implement
• Good performance in many applications
• Highly versatile
• It can be easier to tune
• Can handle steady-state errors

Disadvantages

• Susceptible to noise
• Potential for integral windup
• Complex systems might need additional modifications for performance

PID Controller Tuning Methods

Tuning PID controllers is crucial to ensure optimal performance. Below, we look at several methods on how to tune PID controllers.

Manual Tuning

For this method, you have to adjust the proportional, integral, and derivative gains iteratively while observing the system response. You can refine the settings until you achieve the desired performance.

Start with a low gain and gradually increase the proportional gain until the output responds to the errors. Next, adjust the integral gain to eliminate the steady-state error. Finally, increase the derivative gain to reduce overshoots and oscillations.

Manual tuning can be time-consuming, especially for systems with long loop times.

Ziegler-Nichols Method

This is a classical tuning method that involves either an open-loop step response or a closed-loop response.

In the open-loop method, a step input is applied, and a response is modeled using the first-order plus dead time model. These parameters are now used for calculating the PID gains.

The closed-loop method works by increasing the proportional gain until sustained oscillations occur, and then it calculates the PID gains based on the oscillation period and gain.

Cohen-Coon Method

This is another common method used for open-loop systems. It involves introducing a step change in a manipulated variable and then measuring the response.

The measured data is then used in the pre-defined formula to help calculate the PID parameters.

Rule-Based Tuning

This tuning is based on established methods and assumed process responses to derive mathematical formulas key for calculating PID parameters.

This method often involves experiments used to gather process characteristics, which are then used to calculate the PID settings.

Model-Based Tuning

Still on how to tune PID controllers, we have the model-based tuning as well. This one involves creating a mathematical model for the system and then using it to determine the optimal PID parameters.

Methods such as model predictive control and internal model control fall under this category.

Automatic Tuning

Some PID controllers come with autotuning features. This means the PID gains are automatically adjusted to find the proper performance.

You can utilize software tools like Simulink and MATLAB for automated PID tuning.

結論

あ PID controller is a crucial component of the feedback system in various industrial control loops. It allows for the system to check for errors and adjust accordingly to deliver on the desired setpoint. That is how we find such a system in industrial applications that require precise control and ensure this performance is maintained as well. Tuning may be necessary, which is why various tuning methods are mentioned above. On overall, if you can find the right PID controller and tune it to your needs, expect great performance.

Video: PID Controller Explained